投稿者: daichi kitahara

北原大地/Kitahara Daichi the Researcher
by daichi kitahara

Daichi Kitahara (Member, IEEE), I received the B.E.degree in computer science, and the M.E. and Ph.D.degrees in communications and computer engineering from the Tokyo Institute of Technology, Tokyo, Japan, in 2012, 2014 and 2017, respectively.
Since 2017, I’ve been an Assistant Professorwith the College of Information Science and Engineering, Ritsumeikan University.

The research interests are in signal processing and its applications, inverse problem, optimization theory, and multivariate spline theory.

 

経歴 

長野県出身

1990年生まれ

2008年4月 東京科学大学(旧東京工業大学)工学部５類

　　　　　　(在学中,飛び級の資格を得るが辞退)

2012年4月　東京科学大学(旧東京工業大学)大学院

2014年4月 – 2017年3月日本学術振興会 特別研究員(DC1)

2017年3月　東京科学大学(旧東京工業大学)大学院, 理工学研究科, 通信情報工学専攻

2017年4月　立命館大学 情報理工学部 情報理工学科 助教

2022年4月～ 大阪大学大学院工学研究科 特任研究員

受賞歴

2012年11月SIP若手奨励賞, 電子情報通信学会 基礎境界ソサイエティ 信号処理研究専門委員会

2015年3月部会奨励賞, 計測自動制御学会 計測部門 リモートセンシング部会

2015年12月Young Researcher Award, IEEE Computational Intelligence Society Japan Chapter

2016年4月IEEE SPS Japan Student Journal Paper Award, IEEE Signal Processing Society Tokyo Joint Chapter

2018年2月手島精一記念研究賞（博士論文賞）, 東京工業大学

2018年2月丹羽保次郎記念論文賞, 東京電機大学

他多数

I received the Young Researcher Award from the Institute of Electronics, Information and Communication Engineers (IEICE) Technical Group on Signal Processing in 2013, the Society of Instrument and Control Engineers (SICE) Technical Committee on Remote Sensing in 2015, and the IEEE Computational Intelligence Society Japan Chapter in 2016. I also received the IEEE Signal Processing Society (SPS) Japan Student Journal Paper Award from the IEEE SPS Tokyo Joint Chapter in 2016 and the Yasujiro Niwa Outstanding Paper Award from the Tokyo Denki University in 2018. From 2014 to 2017, I was a recipient of the Research Fellowship of the Japan Society for the Promotion of Science (JSPS).
 

担当講義・授業

Media Project Seminar 1 (Ritsumeikan University)
メディアプロジェクト演習１ (立命館大学)
Computer Exercises in Media Technology (Ritsumeikan University)
メディア計算機演習 (立命館大学)
Probability and Statistics (Ritsumeikan University)
確率・統計 (立命館大学)
Media Project Seminar 2 (Ritsumeikan University)
メディアプロジェクト演習２ (立命館大学)
Basic Mathematics for Media Technology (Ritsumeikan University)
メディア基礎数学 (立命館大学)

 

Academic Background

Apr. 2014–Mar. 2017 Department of Communications and Computer Engineering, Graduate School of Science and Engineering, Tokyo Institute of Technology (Ph.D.)
Apr. 2012–Mar. 2014 Department of Communications and Integrated Systems, Graduate School of Science and Engineering, Tokyo Institute of Technology (M.E.)
Apr. 2008–Mar. 2012 Department of Computer Science, School of Engineering, Tokyo Institute of Technology (B.E.)

Work Experience

Apr. 2017– Assistant Professor at College of Information Science and Engineering, Ritsumeikan University
Apr. 2014–Mar. 2017 Research Fellow (DC1) of the Japan Society for the Promotion of Science (JSPS)

Committee and Society

Oct. 2018– System and Signal Processing Sub-Society, Engineering Sciences Society, IEICE Management Committee of the Workshop on Circuits and Systems
Jun. 2018– System and Signal Processing Sub-Society, Engineering Sciences Society, IEICE Technical Group on Signal Processing

Awards

2019/08 Management Committee of the Workshop on Circuits and Systems, System and Signal Processing Sub-Society, Engineering Sciences Society, IEICE Young Researcher Encouragement Award on the 32nd Workshop on Circuits and Systems
2018/02 Tokyo Denki University Yasujiro NIWA Outstading Paper Award
2018/02 Tokyo Institute of Technology Seiichi Tejima Doctoral Dissertation Award
2016/04 IEEE Signal Processing Society Tokyo Joint Chapter IEEE SPS Japan Student Journal Paper Award
2015/12 IEEE Computational Intelligence Society Japan Chapter Young Researcher Award
2015/03 Technical Committee on Remote Sensing, Division of Measurement, SICE Young Researcher Encouragement Award
2012/11 Technical Group on Signal Processing, System and Signal Processing Sub-Society, Engineering Sciences Society, IEICE Signal Processing Young Researcher Encouragement Award
 
 
音響処理(音響分離/音源信号復元)
by daichi kitahara

音響分離

音源分離とは，複数の音源信号が混合された観測信号から，混合前の各音源信号を推定する技術である．

特に，音源の混合過程に関する事前情報 (音源やマイクの位置など) がほとんど未知である場合には，ブラインド音源分離と呼ばれる．通常は音源やマイクの位置関係は未知である場合が多く，適用できない手法が多い．

 

音源信号の混合過程は，時間領域では畳み込み演算となり取り扱いが難しいため，周波数領域で乗算としてモデル化することが多い．過決定条件
(マイク数 ≥ 音源数) 下におけるブラインド音源分離では，周波数ビンごとに，混合系 (混合行列) の逆写像である分離系 (分離行列) を求める分離手法が数多く提案されている．これらの手法では，音源信号の生成モデルを統計的独立性と優ガウス性 (ガウス関数と比較してピークが鋭い性質) に基づいて設計した上で，最尤推定を行うことで分離行列を決定している….

北原 大地, 小田 亮太, 平林 晃,

“混合過程推定にスパース性を利用したブラインド音源分離,”

第62回システム制御情報学会研究発表講演会, 京都, May 2018, 7 pages.

[Audio Signal Processing, Nonconvex Optimization] pdf (preprint)

 

小田 亮太, 北原 大地, 平林 晃,

“インパルス応答のスパース性を利用したブラインド音源分離,”

電子情報通信学会信号処理研究会, 石垣, Mar. 2018, vol. 117, no. 516, pp. 341–346.

[Audio Signal Processing, Nonconvex Optimization] official access / pdf (preprint)

 

 

音源信号復元

信号の時間周波数解析手段として，スペクトログラムが広く用いられている．近年，音声音響信号処理を中心に，振幅スペクトログラムを加工することで所望の時間信号を生成する技術が注目されている．例えば音源分離の分野では，複数の音源が混在した混合音の振幅スペクトログラムに対して，適切な時間周波数マスクを乗じることで，特定音源のみからなる振幅スペクトログラムを推定する手法が提案されている．

推定した振幅スペクトログラムに適切な位相スペクトログラムを付与できれば，特定音源のみを含む時間信号が復元される．

 

近年，音声音響信号処理において，観測信号を短時間フーリエ変換して得られるスペクトログラムの振幅値を処理し，所望の音源信号を得る手法が数多く開発されている．一方，音楽等の解析に関しては，周波数成分を対数軸上でサンプリングする，定 Q 変換のスペクトログラムが有効である．

しかし，定 Q 変換は逆変換が簡単な閉形式として表現できないため，Griffin–Lim 型のアルゴリズムによって振幅スペクトログラムから音源信号を復元することが困難であった…

 

中津 龍星, 北原 大地, 平林 晃,

“振幅スペクトログラムからの非Griffin–Lim型音源信号復元手法,”

第34回信号処理シンポジウム, 鳥取, Nov. 2019, pp. 162–165.

[Signal Processing Theory and Methods, Audio Signal Processing, Nonconvex Optimization] pdf (preprint)

 

 

カメラと画像ノイズ除去
by daichi kitahara

空間内の各点における各方向の光線の強度分布をライトフィールドという ．

通常の静止画カメラは，イメージセンサ前方から来る無数の光線が合成された際の輝度値を記録する．合成前の各方向から来る光線の輝度値を記録すれば，図 1 のように被写体を異なる視点から眺めた複数枚の画像 (多視点画像群と呼ぶ) が得られる．

他にも，深度推定，デジタルリフォーカス，全焦点画像の作成など，ライトフィールドを利用することで様々な視覚効果を実現できる．

 

ライトフィールドの取得には，カメラを複数用いる方法とカメラを 1 つのみ用いる方法がある．

前者では，複数のカメラを格子状に並べてカメラアレイを構成することで，同一被写体を異なる視点から同時に撮像する．この方法は，カメラアレイが大規模となるため，製造コストや持ち運びの観点であまり実用的ではない．

一方，後者には符号化撮像を用いる方法 とマイクロレンズアレイを用いる方法の 2 種類がある．

 

符号化撮像では，主レンズ (開口面)に光線の透過率を制御するマスクを被せて被写体を撮像し，得られた複数枚の画像から多視点画像群＝ライトフィールドを復元する．この方法では，符号化マスクを取り替えながら被写体を視点数以上の回数撮像する必要があるため，撮像時間全体が長くなり，
被写体も静止物体に限定されるという問題がある．

マイクロレンズアレイを利用したライトフィールドカメラには，例えば米国 Lytro 社のLytro Light Field Camera があり，図 2 に示すような光学系が用いられる．図 2 では，一般的なカメラにおけるセンサ位置 (主レンズの焦点面) にマイクロレンズアレイが，更にその後ろにイメージセンサが設置されている．結果として，イメージセンサの各素子には特定方向から到来する光線の輝度値のみが記録されるようになる．

各視点の画像は主レンズの同一箇所を通過した光線の輝度値から得られるため，単一カメラ・単一撮像でのライトフィールドの取得が可能となる．

ただし，視点数を増やすほど 1 視点あたりのイメージセンサ素子数が減る，つまり画像解像度が低下するというトレードオフの関係がある．

 

 

深度推定やデジタルリフォーカスなどを高精度に行うためには，前処理として取得したライトフィールドに含まれているノイズを除去する必要がある．
Liu らは 3 階テンソルを用いたノイズ除去手法を提案した．この手法では，マルチスペクトル画像用に開発された既存のノイズ除去手法のアイディアを，ライトフィールド用に修正して用いている．しかし，ライトフィールドが持つ特性を十分に考慮しきれておらず，特にマイクロレンズアレイを用いて撮像を行った際には端の視点でノイズ除去性能が大きく劣化してしまう．他にも，グレースケールのライトフィールドのみにしか対応していないという欠点もあった…

 

 

北原 大地, 小川 佳瑚, 金銅 美陽, 平林 晃,

“4階テンソル構造を利用したライトフィールドノイズ除去,”

第33回回路とシステムワークショップ, 岐阜, Aug. 2020, pp. 41–46.

[Image Processing, Nonconvex Optimization] pdf (preprint)

 

スプライン関数と分位点回帰(数学)
by daichi kitahara

スプライン関数とは，微分も含んだ何らかの連続性条件を満たすように設計された，滑らかな区分的多項式のことである．特に，3 次の自然スプライン関数は，ある種の曲率を最小化する最も滑らかな関数となることから，基礎から応用まで幅広い分野で使用されている．

スプライン関数は，何らかの連続性条件を満たすように設計された区分的多項式であり, 連続な区分的多項式の中で，最も単純なものは折れ線グラフとなるが，「スプライン関数」と呼ぶ際には，2 階微分までの連続性を保証した滑らかな曲線を暗に意味する場合が多い．この理由は，現在最もよく使用されている「3 次の自然スプライン関数」が有する性質にある．3 次の自然スプライン関数は，与えられたデータ点を補間する際に，「2 階導関数の L2 ノルム」という意味での曲率を，他のどんなC2 級の関数よりも小さくすることができる．

 

この滑らかさに関する最適性と区分的多項式というモデルの単純性及び柔軟性から，スプライン関数は補間・平滑化・回帰分析といった基本問題から，Computer-Aided Design (CAD)・Computer Graphics (CG) といった応用に至るまで幅広い分野で使われている．

 

北原 大地,

“区分的多項式とスプライン関数の基礎—折れ線グラフを曲線にしてみよう—,”

日本音響学会誌, vol. 78, no. 10, pp. 570–577, Oct. 2022.

[Signal Processing Theory and Methods, Spline Smoothing] official access / pdf (preprint)

北原 大地,

“スプライン関数の基礎と分位点回帰への応用,”

電子情報通信学会信号処理研究会, Online, Aug. 2020, vol. 120, no. 142, pp. 37–42. (招待講演)

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

気象レーダー/高精度ビームフォーミング
by daichi kitahara

気象レーダー

局所的集中豪雨の発生頻度は最近 20 年で有意に増加傾向にあり，被害も甚大なものとなっている ．
この深刻な気象現象の原因は積乱雲であり，高さが10 キロメートルを超えることもある．一方で，発生から消滅までは10分から30分程度と，短時間で状態が大きく移り変わる現象である．

従来のドップラー気象レーダでは，特定の約 10 から 20 の仰角方向にのみペンシルビームを送信し，対象仰角の気象状態を観測する．全方位を観測するためには，アンテナの向きを変えながら観測仰角数と同じ回数アンテナを回転させる必要があり，5 分から 10 分程度の時間がかかってしまう ．

したがって，局所的集中豪雨を観測するには，時間・空間分解能が不十分であった．

 

そのため, 時間・空間分解能向上のために フェーズドアレイ技術とビームフォーミング技術を併用する気象レーダ (Phased Array Weather Radar: PAWR) が開発された．

 

フェーズドアレイ技術によりアンテナの向きを変えることなく瞬時にビームの送信方向を変えることができ，上空の散乱信号をまとめて一度に受信する．そして，受信した混合信号からビームフォーミング技術により各仰角の散乱信号を抽出する．これによりアンテナを 1 回転させるだけで全天の観測が可能となり，観測時間が 10 秒から 30 秒程度と大幅に短縮された．

 

 

北原 大地, 森川 侑奈, 平林 晃, 吉川 栄一, 菊池 博史, 牛尾 知雄,

“フェーズドアレイレーダにおける隣接仰角間の類似性を利用した気象パラメータ推定,”

第32回回路とシステムワークショップ, 東京, Aug. 2019, pp. 129–134.

[Radar Signal Processing, Nonconvex Optimization] pdf (preprint)

 

 

 

D. Kitahara, H. Kuroda, A. Hirabayashi, E. Yoshikawa, H. Kikuchi, and T. Ushio,

“Nonlinear beamforming based on group-sparsities of periodograms for phased array weather radar,”

IEEE Transactions on Geoscience and Remote Sensing, vol. 60, 19 pages, Mar. 2022.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization] official access / pdf (preprint)

 

 

 

滝本 健人, 北原 大地, 平林 晃, 牛尾 知雄,

“フェーズドアレイ気象レーダのための時空間的特徴を利用した高精度ビームフォーミング,”

2020年電子情報通信学会総合大会, 東広島, Mar. 2020, p. 73.

[Radar Signal Processing, Convex Optimization] pdf (preprint)

MRI画像圧縮センシング
by daichi kitahara

MRI

磁気共鳴画像法 (Magnetic Resonance Imaging: MRI)は強力な磁力を利用して生体の内部構造を画像化する装置である．

コンピュータ断層撮影法 (Computed Tomography: CT) と比較して，X 線で被曝しないという利点がある一方で，検査にかかる時間が長いという欠点がある．

 

臨床現場における MRI 検査では，放射線科医が適切な診断を下すのに十分な情報を得るために，一度の検査で繰り返し時間 (TR) とエコー時間 (TE) の設定を変えて複数種類の MR 画像を取得している．取得頻度が高い画像として，解剖学的構造の描出に長けた T1 強調画像と，病変の描出に長けた T2 強調画像があり,どちらも撮像には 2 分から 3 分程度の時間を必要とする．

 

CT は数十秒で撮像を終えることから，患者の負担を考慮して，MRI の撮像時間を短縮することが求められている．
MRI では，観測データを時間軸上で順次取得するため，取得データ数を減らすことで撮像時間を短縮できる．削減された観測データに対して通常の画像再構成手法である逆フーリエ変換を適用すると，アーチファクトを含んだ不鮮明な画像が再構成されてしまう．削減されたデータからも鮮明な画像を再構成するために，圧縮センシング(Compressed Sensing: CS) 理論が利用されている.

 

※圧縮センシング とは，未知の対象信号が適切な表現空間においてスパースになることを利用して，少数の観測信号から対象信号を高精度に復元する技術である.

 

エッジ情報とLiGMEモデルを用いたマルチコントラスト圧縮センシングMRI

MRI は検査に時間がかかるため，取得データ数を減らして撮像時間を短縮した上で，なるべく高精度な画像再構成を目指す，圧縮センシング MRI が研究されている．

臨床現場では一度の検査で複数種類の MR 画像を撮像するが，Ehrhardt らは 1 種類の MR 画像のみ全データを取得してそのエッジ情報を活用する，マルチコントラスト圧縮センシング MRI を提案した．他の種類の画像は，共通のエッジ情報に基づき少数の観測データから高精度に再構成
される．

Ehrhardt らの手法を近年提案されたLiGME モデルに変更することを提案することで，エッジ情報を考慮した全変動がグループℓ0 擬ノルムに近づくため，大きなエッジを復元しやすくなる．実データを用いた実験で，提案法の有効性を示す

 

北原 大地, 加藤 里佳子, 黒田 大貴, 平林 晃,

“エッジ情報とLiGMEモデルを用いたマルチコントラスト圧縮センシングMRI,”

第35回信号処理シンポジウム, 高知, Nov. 2020, pp. 95–100.

[Medical Image Processing, Convex Optimization] pdf (preprint)

柴田 基, 北原 大地, 平林 晃,

“レベル集合制約を用いた圧縮センシングMRI,”

第8回横幹連合コンファレンス, 京都, Dec. 2017, 6 pages.

[Medical Image Processing, Convex Optimization] official access / pdf (preprint)

論文・学会一覧/Publications Conferences
by daichi kitahara

Preprints / Submitted

 

D. Kitahara and K. Yatabe,

“Design of tight minimum-sidelobe windows by Riemannian Newton’s method,”

preprint arXiv:2111.01593, 5 pages, 2021.

[Signal Processing Theory and Methods, Audio Signal Processing, Nonconvex Optimization]

 

D. Kitahara,

“Frequency-undersampled short-time Fourier transform,”

preprint arXiv:2010.15029, 5 pages, 2020.

[Signal Processing Theory and Methods, Audio Signal Processing, Others]

 

 

Journal Papers

[2023]

H. Kuroda, D. Kitahara, E. Yoshikawa, H. Kikuchi, and T. Ushio,

“Convex estimation of sparse-smooth power spectral densities from mixtures of realizations with application to weather radar,”

IEEE Access, vol. 11, pp. 128859–128874, Nov. 2023.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization] official access

 

L. Condat, D. Kitahara, A. Contreras, and A. Hirabayashi,

“Proximal splitting algorithms for convex optimization: A tour of recent advances, with new twists,”

SIAM Review, vol. 65, no. 2, pp. 375–435, May 2023.

[Signal Processing Theory and Methods, Convex Optimization] official access / pdf (preprint)

 

S. Yao, D. Kitahara, H. Kuroda, and A. Hirabayashi,

“Modal interval regression based on spline quantile regression,”

IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol. E106-A, no. 2, pp. 106–123, Feb. 2023.

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

[2022]

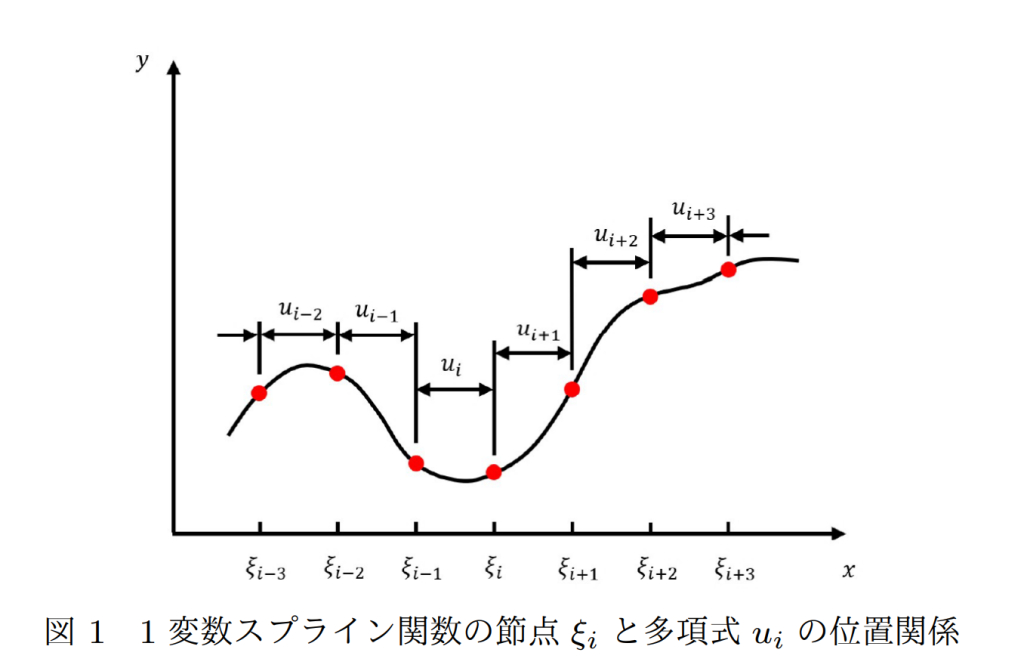
北原 大地,

“区分的多項式とスプライン関数の基礎—折れ線グラフを曲線にしてみよう—,”

日本音響学会誌, vol. 78, no. 10, pp. 570–577, Oct. 2022.

[Signal Processing Theory and Methods, Spline Smoothing] official access / pdf (preprint)

 

H. Yamamoto, D. Kitahara, H. Kuroda, and A. Hirabayashi,

“Image super-resolution via generative adversarial networks using metric projections onto consistent sets for low-resolution inputs,”

IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol. E105-A, no. 4, pp. 704–718, Apr. 2022.

[Image Processing, Machine Learning] official access / pdf (preprint)

 

D. Kitahara, H. Kuroda, A. Hirabayashi, E. Yoshikawa, H. Kikuchi, and T. Ushio,

“Nonlinear beamforming based on group-sparsities of periodograms for phased array weather radar,”

IEEE Transactions on Geoscience and Remote Sensing, vol. 60, 19 pages, Mar. 2022.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization] official access / pdf (preprint)

 

H. Kuroda and D. Kitahara,

“Block-sparse recovery with optimal block partition,”

IEEE Transactions on Signal Processing, vol. 70, pp. 1506–1520, Mar. 2022.

[Signal Processing Theory and Methods, Radar Signal Processing, Audio Signal Processing, Convex Optimization] official access / pdf (preprint)

 

[2021]

K. Yoshimoto, H. Kuroda, D. Kitahara, and A. Hirabayashi,

“WaveNet modeling of distortion pedal using spectral features,”

Acoustical Science and Technology, vol. 42, no. 6, pp. 305–313, Nov. 2021.

[Audio Signal Processing, Machine Learning] official access / pdf

 

H. Kamoshita, D. Kitahara, K. Fujimoto, L. Condat, and A. Hirabayashi,

“Multiclass dictionary-based statistical iterative reconstruction for low-dose CT,”

IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol. E104-A, no. 4, pp. 702–713, Apr. 2021.

[Medical Image Processing, Nonconvex Optimization] official access / pdf (preprint)

 

[2020]

R. Kawami, D. Kitahara, A. Hirabayashi, E. Yoshikawa, H. Kikuchi, and T. Ushio,

“Three-dimensional data compression and fast high-quality reconstruction for phased array weather radar,”

IEEJ Transactions on Electronics, Information and Systems, vol. 140, no. 1, pp. 40–48, Jan. 2020.

[Radar Signal Processing, Convex Optimization] official access / pdf (preprint)

[2019]

[2018]

[2017]

平林 晃, 北原 大地,

“圧縮センシングの基礎と画像取得への応用,”

光学, vol. 46, no. 10, pp. 393–397, Oct. 2017.

[Image Processing, Medical Image Processing, Convex Optimization, Nonconvex Optimization] official access / pdf (preprint)

 

[2016]

D. Kitahara and I. Yamada,

“Algebraic phase unwrapping based on two-dimensional spline smoothing over triangles,”

IEEE Transactions on Signal Processing, vol. 64, no. 8, pp. 2103–2118, Apr. 2016.

[Signal Processing Theory and Methods, Radar Signal Processing, Polynomial Algebra, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

[2015]

D. Kitahara and I. Yamada,

“Algebraic phase unwrapping along the real axis: extensions and stabilizations,”

Multidimensional Systems and Signal Processing, vol. 26, no. 1, pp. 3–45, Jan. 2015.

[Signal Processing Theory and Methods, Polynomial Algebra] official access / pdf (preprint)

 

 

国際学会/International Conferences

[2023]

H. Kuroda, D. Kitahara, E. Yoshikawa, H. Kikuchi, and T. Ushio,

“Sparsity-smoothness-aware power spectral density estimation with application to phased array weather radar,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, Jun. 2023, to appear.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization]

 

[2022]

H. Kuroda and D. Kitahara,

“Graph-structured sparse regularization via convex optimization,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, May 2022, pp. 5538–5542.

[Signal Processing Theory and Methods, Convex Optimization] official access

 

[2021]

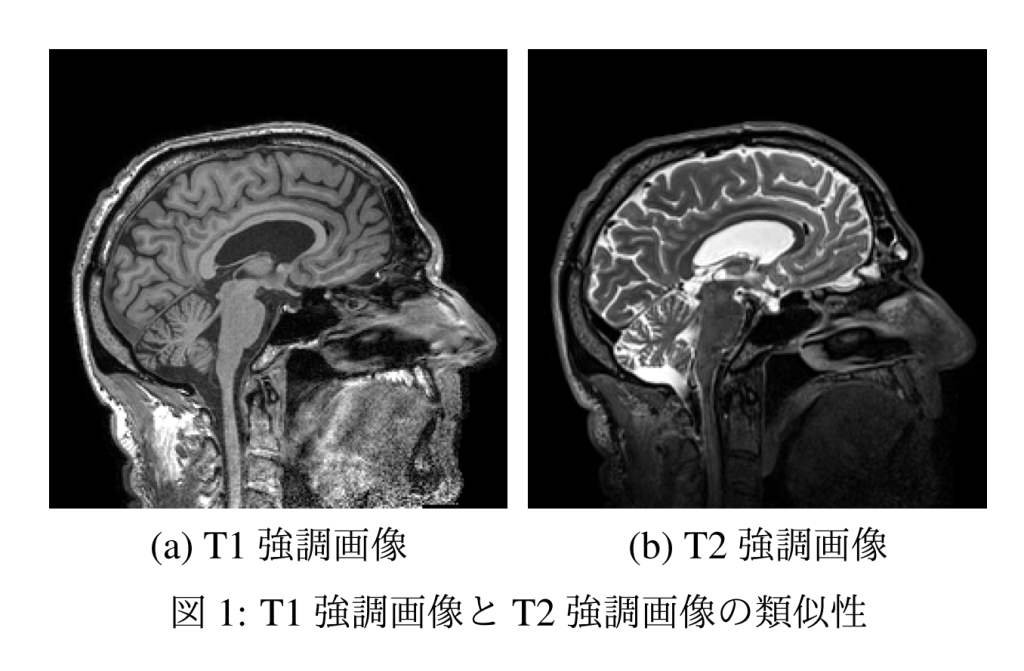
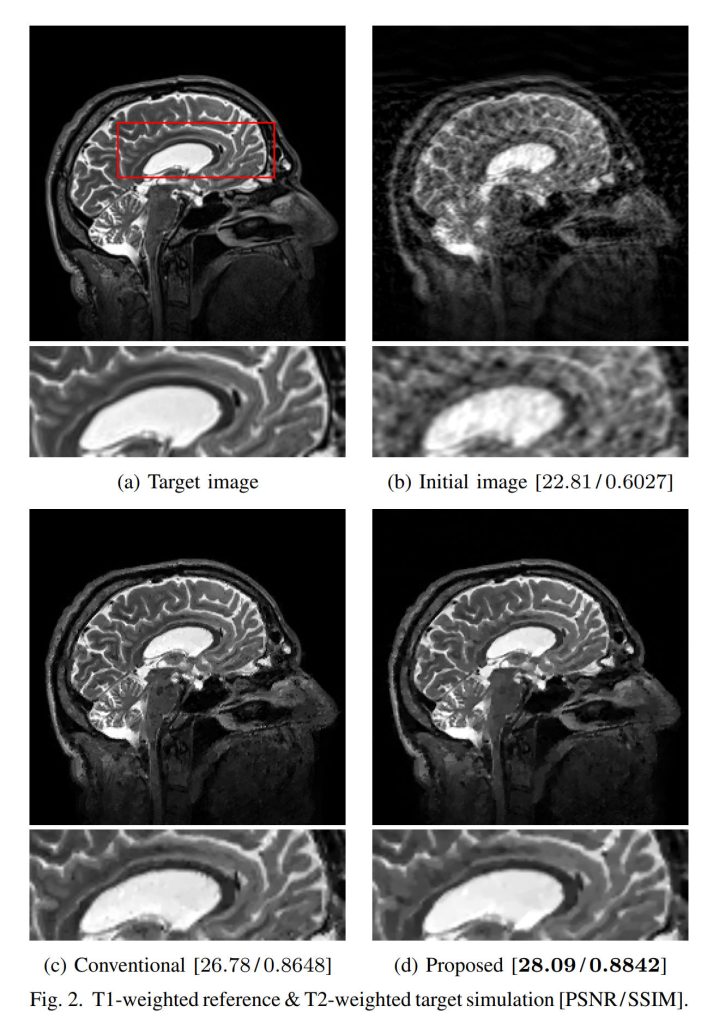
D. Kitahara, R. Kato, H. Kuroda, and A. Hirabayashi,

“Multi-contrast CSMRI using common edge structures with LiGME model,”

European Signal Processing Conference (EUSIPCO), Dublin, Ireland, Aug. 2021, pp. 2119–2123.

[Medical Image Processing, Convex Optimization] official access / pdf (preprint)

 

H. Kuroda, D. Kitahara, and A. Hirabayashi,

“A convex penalty for block-sparse signals with unknown structures,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, Canada, Jun. 2021, pp. 5430–5434.

[Signal Processing Theory and Methods, Radar Signal Processing, Audio Signal Processing, Convex Optimization] official access / pdf

 

[2020]

K. Yoshimoto, H. Kuroda, D. Kitahara, and A. Hirabayashi,

“Deep neural network modeling of distortion stomp box using spectral features,”

Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Auckland, New Zealand, Dec. 2020, pp. 339–345.

[Audio Signal Processing, Machine Learning] official access / pdf (preprint)

 

D. Kitahara, K. Leng, Y. Tezuka, and A. Hirabayashi,

“Simultaneous spline quantile regression under shape constraints,”

European Signal Processing Conference (EUSIPCO), Amsterdam, Netherlands, Oct. 2020, pp. 2423–2427.

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

H. Yamamoto, D. Kitahara, and A. Hirabayashi,

“Image super-resolution via generative adversarial network using an orthogonal projection,”

European Signal Processing Conference (EUSIPCO), Amsterdam, Netherlands, Oct. 2020, pp. 660–664.

[Image Processing, Machine Learning] official access / pdf (preprint)

 

R. Nakatsu, D. Kitahara, and A. Hirabayashi,

“Non-Griffin–Lim type signal recovery from magnitude spectrogram,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, May 2020, pp. 791–795.

[Signal Processing Theory and Methods, Audio Signal Processing, Nonconvex Optimization] official access / pdf (preprint)

 

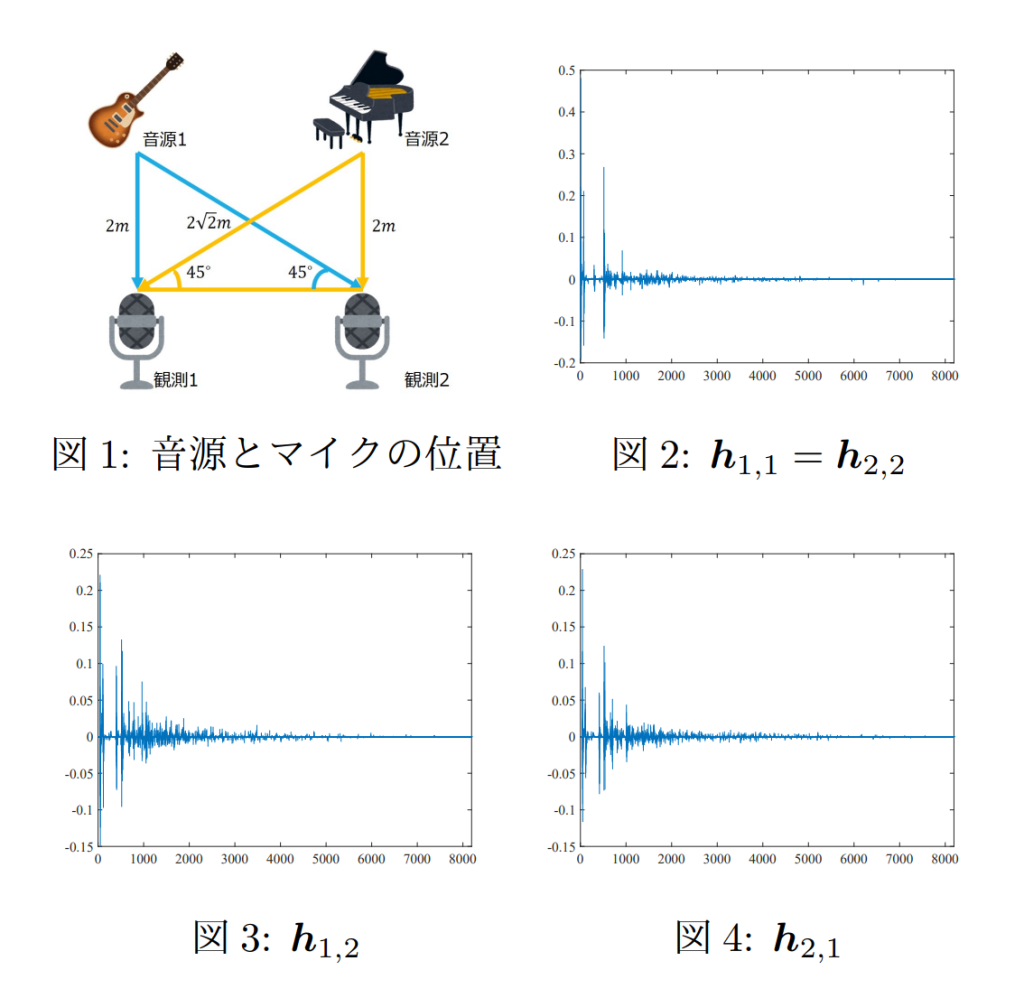
Y. Takahashi, D. Kitahara, K. Matsuura, and A. Hirabayashi,

“Determined source separation using the sparsity of impulse responses,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, May 2020, pp. 686–690.

[Audio Signal Processing, Nonconvex Optimization] official access / pdf (preprint)

 

[2019]

S. Ananda, D. Kitahara, A. Hirabayashi, and K. R. U. K. Reddy,

“Automatic fundus image segmentation for diabetic retinopathy diagnosis by multiple modified U-Nets and SegNets,”

Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Lanzhou, China, Nov. 2019, pp. 1582–1588.

[Medical Image Processing, Machine Learning] official access / pdf (preprint)

 

D. Kitahara, S. Ananda, and A. Hirabayashi,

“Optimization-based fundus image decomposition for diagnosis support of diabetic retinopathy,”

Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Lanzhou, China, Nov. 2019, pp. 1565–1572.

[Medical Image Processing, Convex Optimization] official access / pdf (preprint)

 

H. Kamoshita, T. Shibata, D. Kitahara, K. Fujimoto, and A. Hirabayashi,

“Low-dose CT reconstruction with multiclass orthogonal dictionaries,”

IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, Sep. 2019, pp. 2055–2059.

[Medical Image Processing, Nonconvex Optimization] official access / pdf (preprint)

 

D. Kitahara, L. Condat, and A. Hirabayashi,

“One-dimensional edge-preserving spline smoothing for estimation of piecewise smooth functions,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, May 2019, pp. 5611–5615.

[Signal Processing Theory and Methods, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

L. Condat, D. Kitahara, and A. Hirabayashi,

“A convex lifting approach to image phase unwrapping,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, May 2019, pp. 1852–1856.

[Signal Processing Theory and Methods, Image Processing, Medical Image Processing, Radar Signal Processing, Convex Optimization] official access / pdf

 

[2018]

D. Kitahara, M. Nakahara, A. Hirabayashi, E. Yoshikawa, H. Kikuchi, and T. Ushio,

“Nonlinear beamforming via convex optimization for phased array weather radar,”

Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Honolulu, HI, USA, Nov. 2018, pp. 1831–1835.

[Radar Signal Processing, Convex Optimization] official access / pdf (preprint)

 

D. Kitahara and I. Yamada,

“A branch cut algorithm for 180-degree ambiguity resolution in 2D vector fields and its application to single-frame fringe projection profilometry,”

Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Honolulu, HI, USA, Nov. 2018, pp. 122–128.

[Signal Processing Theory and Methods, Image Processing, Combinatorial Optimization] official access / pdf (preprint)

 

[2017]

R. Kawami, H. Kataoka, D. Kitahara, A. Hirabayashi, T. Ijiri, S. Shimamura, H. Kikuchi, and T. Ushio,

“Fast high-quality three-dimensional reconstruction from compressive observation of phased array weather radar,”

Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, Dec. 2017, pp. 44–49.

[Radar Signal Processing, Convex Optimization] official access / pdf (preprint)

 

D. Kitahara and I. Yamada,

“Algebraic phase unwrapping with self-reciprocal polynomial algebra,”

International Conference on Sampling Theory and Applications (SampTA), Tallinn, Estonia, Jul. 2017, pp. 350–354.

[Signal Processing Theory and Methods, Polynomial Algebra] official access / pdf (preprint)

 

[2016]

M. Yamagishi, D. Kitahara, and I. Yamada,

“A fast dual iterative algorithm for convexly constrained spline smoothing,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, Mar. 2016, pp. 4538–4542.

[Signal Processing Theory and Methods, Spline Smoothing, Convex Optimization] official access / pdf

 

D. Kitahara and I. Yamada,

“Two-dimensional positive spline smoothing and its application to probability density estimation,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, Mar. 2016, pp. 4219–4223.

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

K. Kakimoto, D. Kitahara, M. Yamagishi, and I. Yamada,

“Stabilization of adaptive eigenvector extraction by continuation in nested orthogonal complement structure,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, Mar. 2016, pp. 4189–4193.

[Signal Processing Theory and Methods, Others] official access / pdf

 

[2015]

D. Kitahara, M. Yamagishi, and I. Yamada,

“A virtual resampling technique for algebraic two-dimensional phase unwrapping,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, Apr. 2015, pp. 3871–3875.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization] official access / pdf (preprint)

 

D. Kitahara and I. Yamada,

“Probability density function estimation by positive quartic C2-spline functions,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, Apr. 2015, pp. 3556–3560.

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

[2014]

D. Kitahara and I. Yamada,

“Algebraic phase unwrapping over collection of triangles based on two-dimensional spline smoothing,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, May 2014, pp. 4963–4967.

[Signal Processing Theory and Methods, Radar Signal Processing, Polynomial Algebra, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

[2013]

D. Kitahara and I. Yamada,

“Algebraic phase unwrapping for functional data analytic estimations—extensions and stabilizations,”

IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, Canada, May 2013, pp. 5835–5839.

[Signal Processing Theory and Methods, Polynomial Algebra] official access / pdf (preprint)

 

 

国内学会/Domestic Conferences

[2022]

H. Kuroda, D. Kitahara, E. Yoshikawa, H. Kikuchi, and T. Ushio,

“Sparsity and smoothness regularized estimation of power spectral density and its application to weather radar,”

第37回信号処理シンポジウム, 新潟, Dec. 2022, pp. 113–117.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization] pdf

 

D. K. Kim, P. Baron, K. Kawashima, D. Kitahara, T. Mega, Y. Wada, and T. Ushio,

日本気象学会2022年度秋季大会, 札幌, Oct. 2022, 1 page, to appear.

[Radar Signal Processing, Machine Learning]

 

川島 康平, 北原 大地, 金 東均, 妻鹿 友昭, 和田 有希, 牛尾 知雄, Philippe Baron, 吉川 栄一, 林 修吾, 菊池 博史,

日本気象学会2022年度秋季大会, 札幌, Oct. 2022, 1 page, to appear.

[Radar Signal Processing, Machine Learning]

 

D. Kitahara and K. Yatabe,

“Design of tight minimum-sidelobe windows by Newton’s method on oblique manifolds for time-frequency domain signal processing,”

日本応用数理学会2022年度年会, 札幌, Sep. 2022, 2 pages.

[Signal Processing Theory and Methods, Audio Signal Processing, Nonconvex Optimization] pdf (preprint)

 

少路 春希, 吉本 健人, 阪 大樹, 黒田 大貴, 北原 大地, 田中 賢一郎, 平林 晃,

“ファインチューニングを利用した歪みエフェクタの高速モデリング,”

電子情報通信学会信号処理研究会, 那覇, Mar. 2022, vol. 121, no. 384, pp. 70–75.

[Audio Signal Processing, Machine Learning] official access / pdf (preprint)

 

[2021]

H. Kuroda and D. Kitahara,

“Exploiting graph-structured sparsity via convex optimization,”

第36回信号処理シンポジウム, Online, Nov. 2021, pp. 92–95.

[Signal Processing Theory and Methods, Convex Optimization] pdf

 

[2020]

H. Kuroda, D. Kitahara, and A. Hirabayashi,

“Recovery of block-sparse signals with optimization of block partitions,”

第35回信号処理シンポジウム, 高知, Nov. 2020, pp. 123–124.

[Signal Processing Theory and Methods, Convex Optimization] pdf

 

北原 大地, 加藤 里佳子, 黒田 大貴, 平林 晃,

“エッジ情報とLiGMEモデルを用いたマルチコントラスト圧縮センシングMRI,”

第35回信号処理シンポジウム, 高知, Nov. 2020, pp. 95–100.

[Medical Image Processing, Convex Optimization] pdf (preprint)

 

北原 大地,

“周波数間引き短時間フーリエ変換の提案,”

第35回信号処理シンポジウム, 高知, Nov. 2020, pp. 11–16.

[Signal Processing Theory and Methods, Audio Signal Processing, Others] pdf (preprint)

 

北原 大地,

“スプライン関数の基礎と分位点回帰への応用,”

電子情報通信学会信号処理研究会, Online, Aug. 2020, vol. 120, no. 142, pp. 37–42. (招待講演)

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

北原 大地, 小川 佳瑚, 金銅 美陽, 平林 晃,

“4階テンソル構造を利用したライトフィールドノイズ除去,”

第33回回路とシステムワークショップ, 岐阜, Aug. 2020, pp. 41–46.

[Image Processing, Nonconvex Optimization] pdf (preprint)

 

滝本 健人, 北原 大地, 平林 晃, 牛尾 知雄,

“フェーズドアレイ気象レーダのための時空間的特徴を利用した高精度ビームフォーミング,”

2020年電子情報通信学会総合大会, 東広島, Mar. 2020, p. 73.

[Radar Signal Processing, Convex Optimization] pdf (preprint)

 

吉本 健人, 北原 大地, 平林 晃,

“スペクトル特徴量を利用した深層学習による歪みエフェクタの高精度モデリング,”

電子情報通信学会信号処理研究会, 那覇, Mar. 2020, vol. 119, no. 440, pp. 135–140.

[Audio Signal Processing, Machine Learning] official access / pdf

 

[2019]

D. Kitahara, K. Leng, Y. Tezuka, and A. Hirabayashi,

“Functional data analysis between two random variables by multilevel monotone splines,”

第34回信号処理シンポジウム, 鳥取, Nov. 2019, pp. 248–251.

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] pdf (preprint)

 

中津 龍星, 北原 大地, 平林 晃,

“振幅スペクトログラムからの非Griffin–Lim型音源信号復元手法,”

第34回信号処理シンポジウム, 鳥取, Nov. 2019, pp. 162–165.

[Signal Processing Theory and Methods, Audio Signal Processing, Nonconvex Optimization] pdf (preprint)

 

松浦 功一郎, 平林 晃, 北原 大地,

“マルチトラック楽曲におけるGANを用いた大楽節の自動生成,”

日本音響学会2019年秋季研究発表会, 草津, Sep. 2019, pp. 1147–1150.

[Audio Signal Processing, Machine Learning] pdf

 

髙橋 悠希, 北原 大地, 平林 晃,

“インパルス応答のスパース性を用いた教師あり独立低ランク行列分析,”

日本音響学会2019年秋季研究発表会, 草津, Sep. 2019, pp. 291–294.

[Audio Signal Processing, Nonconvex Optimization] pdf (preprint)

 

北原 大地, 森川 侑奈, 平林 晃, 吉川 栄一, 菊池 博史, 牛尾 知雄,

“フェーズドアレイレーダにおける隣接仰角間の類似性を利用した気象パラメータ推定,”

第32回回路とシステムワークショップ, 東京, Aug. 2019, pp. 129–134.

[Radar Signal Processing, Nonconvex Optimization] pdf (preprint)

 

北原 大地, 手塚 祐司, 関根 理, 冷 可, 姚 賽, 東 長佳, 山本 有香子, 小林 純, 鷲山 美樹, 巖西 真規, 平林 晃, 柏木 厚典,

“2型糖尿病患者における性差を考慮したBMIと残余リスクの管理状況の関係,”

第62回日本糖尿病学会年次学術集会, 仙台, May 2019, 1 page.

[Data Analysis, Statistical Hypothesis Testing]

 

山本 宏哉, 北原 大地, 平林 晃,

“客観品質を考慮した敵対的生成ネットワークによる画像超解像,”

電子情報通信学会信号処理研究会, 長崎, Mar. 2019, vol. 118, no. 496, pp. 93–98.

[Image Processing, Machine Learning] official access / pdf (preprint)

 

中本 和磨, 藤井 皓介, 北原 大地, 平林 晃,

“2種類の辞書とBCCB行列の対角化を利用したMR画像再構成,”

電子情報通信学会信号処理研究会, 長崎, Mar. 2019, vol. 118, no. 496, pp. 75–80.

[Medical Image Processing, Nonconvex Optimization] official access / pdf (preprint)

 

[2018]

川見 亮介, 北原 大地, 平林 晃, 吉川 栄一, 菊池 博史, 牛尾 知雄,

“フェーズドアレイ気象レーダのデータ圧縮と3階テンソル辞書学習を用いた高精度再構成,”

第33回信号処理シンポジウム, 東京, Nov. 2018, pp. 227–228.

[Radar Signal Processing, Nonconvex Optimization] pdf (preprint)

 

藤井 皓介, 中田 和希, 北原 大地, 平林 晃,

“2種類の直交辞書を用いたMR画像高精度再構成,”

第33回信号処理シンポジウム, 東京, Nov. 2018, pp. 219–224.

[Medical Image Processing, Nonconvex Optimization] pdf (preprint)

 

D. Kitahara, L. Condat, and A. Hirabayashi,

“1D piecewise smooth function estimation with spline functions,”

第33回信号処理シンポジウム, 東京, Nov. 2018, pp. 154–157.

[Signal Processing Theory and Methods, Spline Smoothing, Convex Optimization] pdf (preprint)

 

D. Kitahara, A. Hirabayashi, E. Yoshikawa, H. Kikuchi, and T. Ushio,

“Nonlinear beamforming based on group sparsity for phased array weather radar,”

第33回信号処理シンポジウム, 東京, Nov. 2018, pp. 148–153.

[Radar Signal Processing, Convex Optimization] pdf (preprint)

 

冷 可, 姚 賽, 荒木 はなこ, 北原 大地, 平林 晃, 伊波 早苗, 手塚 祐司, 巌西 真規, 柏木 厚典,

“湖南地域における2型糖尿病患者の特性の解明―肥満と2型糖尿病管理について―,”

第55回日本糖尿病学会近畿地方会, 神戸, Oct. 2018, 1 page.

[Data Analysis, Statistical Hypothesis Testing]

 

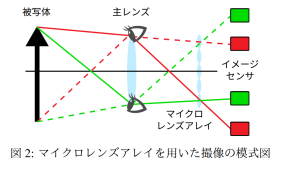
北原 大地, 杉浦 紫緒里, 平林 晃,

“量子化された符号化撮像からの高精度ライトフィールド再構成,”

第24回画像センシングシンポジウム, 横浜, Jun. 2018, 7 pages.

[Image Processing, Convex Optimization] pdf (preprint)

 

鴨下 飛竜, 北原 大地, 平林 晃,

“マルチクラス辞書学習を用いた低線量CT画像再構成,”

電子情報通信学会信号処理研究会, 岐阜, May 2018, vol. 118, no. 33, pp. 63–68.

[Medical Image Processing, Nonconvex Optimization] official access / pdf (preprint)

 

北原 大地, 小田 亮太, 平林 晃,

“混合過程推定にスパース性を利用したブラインド音源分離,”

第62回システム制御情報学会研究発表講演会, 京都, May 2018, 7 pages.

[Audio Signal Processing, Nonconvex Optimization] pdf (preprint)

 

馬場 敦之, 片岡 秀公, 北原 大地, 平林 晃,

“直交射影層を用いた畳み込みニューラルネットワークによる画像超解像,”

電子情報通信学会信号処理研究会, 石垣, Mar. 2018, vol. 117, no. 516, pp. 347–352.

[Image Processing, Machine Learning] official access / pdf (preprint)

 

小田 亮太, 北原 大地, 平林 晃,

“インパルス応答のスパース性を利用したブラインド音源分離,”

電子情報通信学会信号処理研究会, 石垣, Mar. 2018, vol. 117, no. 516, pp. 341–346.

[Audio Signal Processing, Nonconvex Optimization] official access / pdf (preprint)

 

[2017]

柴田 基, 北原 大地, 平林 晃,

“レベル集合制約を用いた圧縮センシングMRI,”

第8回横幹連合コンファレンス, 京都, Dec. 2017, 6 pages.

[Medical Image Processing, Convex Optimization] official access / pdf (preprint)

 

柴田 基, 北原 大地, 平林 晃,

“圧縮サンプリングからのパラメータ設定に頑健なMR画像再構成法,”

第32回信号処理シンポジウム, 盛岡, Nov. 2017, pp. 105–110.

[Medical Image Processing, Convex Optimization] pdf (preprint)

 

D. Kitahara and I. Yamada,

“A stabilization of algebraic phase unwrapping along the unit circle with self-reciprocal subresultant,”

2017年電子情報通信学会総合大会, 名古屋, Mar. 2017, p. 101.

[Signal Processing Theory and Methods, Polynomial Algebra] pdf (preprint)

 

[2016]

森 和也, 北原 大地, 山岸 昌夫, 山田 功,

“Huber損失関数を用いたロバストな三重位相差型GPS,”

第31回信号処理シンポジウム, 吹田, Nov. 2016, pp. 427–432.

[Radar Signal Processing, Convex Optimization] pdf (preprint)

 

D. Kitahara and I. Yamada,

“A branch cut type sign estimator for single-frame fringe projection profilometry,”

第31回信号処理シンポジウム, 吹田, Nov. 2016, pp. 157–161.

[Signal Processing Theory and Methods, Image Processing, Combinatorial Optimization] pdf (preprint)

 

山田 功, 北原 大地,

“位相をつなぐ―代数的位相アンラップとその応用,”

2016年電子情報通信学会ソサイエティ大会, 札幌, Sep. 2016, pp. SS14–SS15. (招待講演)

[Signal Processing Theory and Methods, Polynomial Algebra] official access / pdf

 

D. Kitahara and I. Yamada,

“A branch cut type sign estimator for 3D measurement from a single fringe pattern,”

第9回コンピューテーショナル・インテリジェンス研究会, 千葉, Jul. 2016, pp. 73–76.

[Signal Processing Theory and Methods, Image Processing, Combinatorial Optimization] official access / pdf (preprint)

 

[2015]

D. Kitahara and I. Yamada,

“Algebraic phase unwrapping based on two-dimensional spline smoothing,”

第8回コンピューテーショナル・インテリジェンス研究会, 広島, Dec. 2015, pp. 11–18.

[Signal Processing Theory and Methods, Radar Signal Processing, Polynomial Algebra, Spline Smoothing, Convex Optimization] official access / pdf (preprint)

 

D. Kitahara and I. Yamada,

“Two-dimensional phase unwrapping based on selective smoothing and inconsistency correction,”

第30回信号処理シンポジウム, いわき, Nov. 2015, pp. 361–366.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization] pdf (preprint)

 

D. Kitahara and I. Yamada,

“Positive quartic and biquartic C2-splines and their applications to two-dimensional probability density estimation,”

第30回信号処理シンポジウム, いわき, Nov. 2015, pp. 344–349.

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] pdf (preprint)

 

K. Kakimoto, D. Kitahara, M. Yamagishi, and I. Yamada,

“On a projection step by generalized orthogonal complement matrices for adaptive subspace tracking,”

第30回信号処理シンポジウム, いわき, Nov. 2015, pp. 328–331.

[Signal Processing Theory and Methods, Others] pdf

 

D. Kitahara and I. Yamada,

“A smoothness-aware phase unwrapping by convex optimization technique,”

第40回リモートセンシングシンポジウム, 東京, Mar. 2015, pp. 1–2.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization] pdf (preprint)

 

[2014]

D. Kitahara and I. Yamada,

“One-dimensional probability density function estimation by positive quartic C2-spline interpolation and smoothing,”

第29回信号処理シンポジウム, 京都, Nov. 2014, pp. 462–467.

[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] pdf (preprint)

 

D. Kitahara, M. Yamagishi, and I. Yamada,

“A preprocessing using convex optimization for algebraic two-dimensional phase unwrapping,”

第29回信号処理シンポジウム, 京都, Nov. 2014, pp. 369–374.

[Signal Processing Theory and Methods, Radar Signal Processing, Convex Optimization] pdf (preprint)

 

M. Yamagishi, D. Kitahara, and I. Yamada,

“A fast Gauss–Seidel-like splitting algorithm for convexly constrained spline smoothing,”

第29回信号処理シンポジウム, 京都, Nov. 2014, pp. 64–67.

[Signal Processing Theory and Methods, Spline Smoothing, Convex Optimization] pdf

 

北原 大地,

“二次元位相アンラップ問題の難しさと面白さ,”

第29回信号処理シンポジウム, 京都, Nov. 2014. (チュートリアル講演)

[Signal Processing Theory and Methods, Combinatorial Optimization]

 

[2013]

D. Kitahara and I. Yamada,

“Algebraic phase unwrapping over collection of triangles and its application,”

第28回信号処理シンポジウム, 下関, Nov. 2013, pp. 355–358.

[Signal Processing Theory and Methods, Radar Signal Processing, Polynomial Algebra, Spline Smoothing] pdf (preprint)

 

[2012]

D. Kitahara and I. Yamada,

“A stabilization of algebraic phase unwrapping by subresultant,”

第27回信号処理シンポジウム, 石垣, Nov. 2012, pp. 484–488.

[Signal Processing Theory and Methods, Polynomial Algebra] pdf (preprint)

 

D. Kitahara and I. Yamada,

“A robust algebraic phase unwrapping based on spline approximation,”

電子情報通信学会信号処理研究会, 京都, Jul. 2012, vol. 112, no. 115, pp. 1–6.

[Signal Processing Theory and Methods, Polynomial Algebra, Spline Smoothing] official access / pdf (preprint)

 

D. Kitahara and I. Yamada,

“Mixed trigonometric interpolation techniques for fast and stable algebraic phase unwrapping,”

電子情報通信学会信号処理研究会, 新潟, Mar. 2012, vol. 111, no. 466, pp. 303–307.

[Signal Processing Theory and Methods, Others] official access / pdf (preprint)

 

[2011]

D. Kitahara and I. Yamada,

“A stable sign estimation for algebraic phase unwrapping,”

第26回信号処理シンポジウム, 札幌, Nov. 2011, pp. 562–565.

[Signal Processing Theory and Methods, Others] pdf (preprint)

学生向けQ&A
by daichi kitahara

情報理工学の魅力・面白さとは、どのような点にあると思われますか？

情報理工学部の魅力は何と言っても、自身のアイディアをプログラムによって具現化する能力を修得できる点です。つまり、1台のパソコンのみで、便利なソフトウェアを開発したり、世界中の誰も考えたことのない事象について検証したりできるようになるということです。そのため、情報理工学部では、「学生がお菓子を食べながらくつろいでいるその横で、パソコンが発熱しながら世界初のプログラムをまさに実行している」というシュールな光景がたびたび見受けられます。

 

卒業後、情報理工学部で学んだことはどのように役立つでしょうか？

急速に情報化が進んでいる現代社会において、情報理工学部で学んだ知識を全く必要としない業界を挙げることは極めて困難です。程度の差こそあれ、情報通信技術が活躍している領域がどんな業界においてもあると思います。逆に言えば、情報理工学部で教わる知識や技術を自分のものにすることが出来れば、あるゆる業界において活躍できる可能性を持つことになります。

 

代表的な研究・活動内容、現在の研究テーマについて、教えてください。

一般に、「n個の未知数」（原信号）に対して「n個以上の観測値」が得られれば、未知数と観測値に関する連立方程式から原信号を推定することができます。しかし実際には、「n個未満の観測値」しか得られない状況も数多く存在し、この時に原信号を推定する問題（「劣決定逆問題」と言います）を如何にして解くかが理学・工学上の重要な研究課題となっています。劣決定逆問題に対しても良好な推定結果を得るために、私は観測値に関する連立方程式だけでなく、原信号に関する先験的性質も考慮した「最適化基準」を新たに設計し、それを最もよく満たす信号を原信号の推定値とするアプローチをとっています。

？

 

これから入学する学生に、どんなことを期待されますか？どう成長してもらいたいですか？

昨今はAI（人工知能）ブームもあり情報系の人材に対する需要が高まっているので、情報理工学部の学生は引く手あまただと思います。しかしながら、ブームはいつか終焉を迎えるものですから、これから入学する学生には「時代の流行り廃りに翻弄されない、いつの時代にも通用する確かな能力」を何か1つでも培って欲しいと思います。

 

主に研究で使用するソフトウェア/プログラミング言語は何ですか

アメリカ合衆国のMathWorks社が開発している数値解析ソフトウェアでありプログラミング言語のMATLABを主として利用します。