・北原研は,最適化・信号処理・データサイエンス分野で理論研究や深層学習も含む応用研究を行っています.
・様々な分野の逆問題を横断的に解決する革新的アルゴリズムの創造や,最先端数理の実データへの適用と運用システムへの導入を目指しています.
数理最適化とは?
・数理最適化とは,与えられた関数 \(f(\boldsymbol{x})\) を最小(または最大)にする引数 \(\boldsymbol{x}\) を求めることです.多くの場合,引数 \(\boldsymbol{x}\) は多変数(多次元ベクトル)です.
・\(\boldsymbol{x}\) に制約条件(\(\boldsymbol{x}\) が満たすべき性質)が課されることもあり,最適化問題は一般に以下のように表されます.
\[\underset{\boldsymbol{x}}{\text{minimize}}\ f(\boldsymbol{x})\qquad\mathrm{subject\ to\ }\,\boldsymbol{x}\in C\]
\(C\) は制約条件を満たす全ての \(\boldsymbol{x}\) から成る集合です.
・最適化問題を適切に構築した上で,その(大域的または局所的な)最適解 \(\boldsymbol{x}^{\star}\) を求めることで,従来よりも高精度な信号推定・信号解析を実現できます.
深層学習との関連は?
・深層学習で使うニューラルネットワークは,線形写像(内積計算・畳み込みなど)と比較的簡単な非線形写像(活性化・プーリング・アテンションなど)が幾重にも連なった非常に複雑な合成写像です.
・非線形写像の部分は事前に設定した仕様で固定されることが多く,線形写像の部分に相当する行列やテンソルの各成分が学習可能なパラメータ \(\theta\) です.
・ニューラルネットワークは \(\theta\) をパラメータとする写像 \(g_{\theta}\) となり,以下のような最適化問題の解 \(\theta^{\star}\) を(近似的に)求めることで \(g_{\theta}\) の学習が終了します.
\[\underset{\theta}{\text{minimize}}\ L(g_{\theta})\]
\(L\) は与えられた学習データに基づいて \(g_{\theta}\) の良し悪しを評価する目的関数(損失関数)です.
・通常の最適化と異なる点は,目的関数が学習データを用いて計算される点と,最適解 \(\theta^{\star}\) よりも写像 \(g_{\theta^{\star}}\) の方に興味がある点です.このため,求めた解 \(\theta^{\star}\) の厳密性よりも学習後の写像 \(g_{\theta^{\star}}\) の性能を重視することが多いです.
研究事例
・最適化や深層学習の応用範囲は今なお拡大しており,北原研も既に様々な分野で成果を上げています.
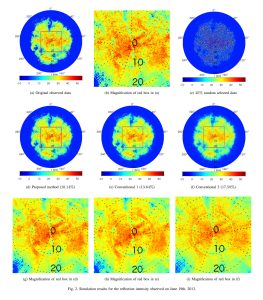
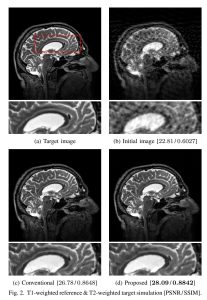
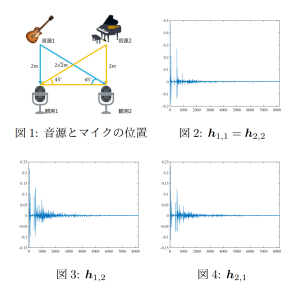
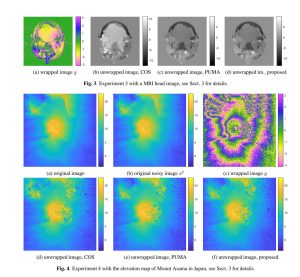
・基礎信号処理(スパース信号復元・非負値関数推定・ロバスト回帰など),画像処理(超解像・CT/MR画像再構成など),音信号処理(STFT用の窓関数設計・スペクトログラム位相回復・歪みエフェクタモデリングなど),レーダ信号処理(合成開口レーダによる標高推定・気象レーダによる降雨推定や予測など)といった広範な研究分野で成果を上げ,知見を蓄えています.
・多くの研究テーマで凸最適化(目的関数 \(f\) が凸で制約集合 \(C\) も凸)を用いており,多くの問題がこちらの論文の凸最適化アルゴリズムで解けます.