スプライン関数とは,微分も含んだ何らかの連続性条件を満たすように設計された,滑らかな区分的多項式のことである.特に,3 次の自然スプライン関数は,ある種の曲率を最小化する最も滑らかな関数となることから,基礎から応用まで幅広い分野で使用されている.
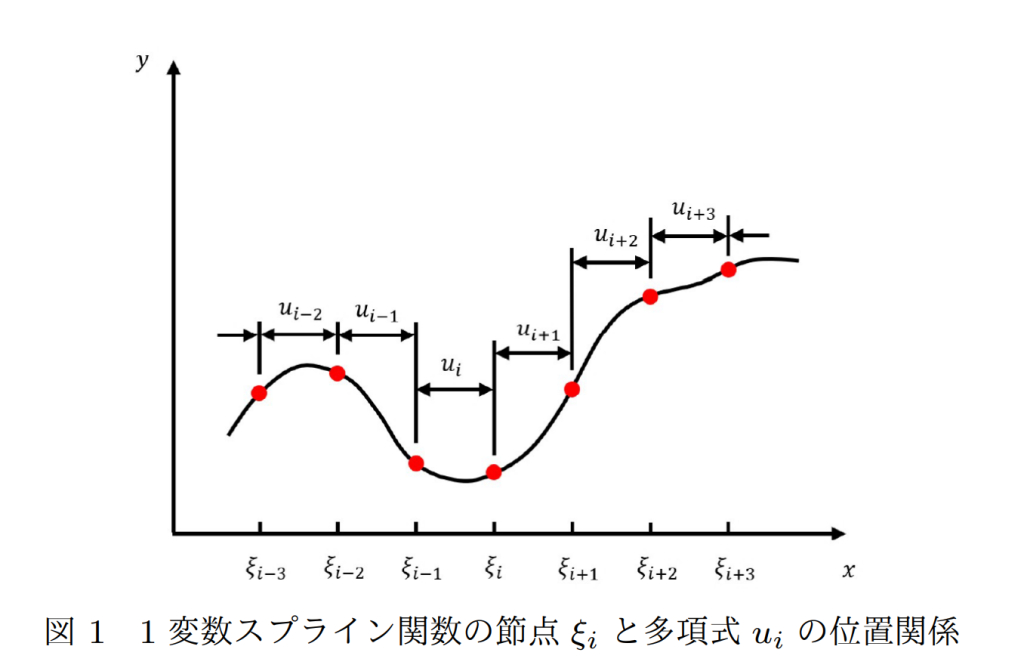
スプライン関数は,何らかの連続性条件を満たすように設計された区分的多項式であり, 連続な区分的多項式の中で,最も単純なものは折れ線グラフとなるが,「スプライン関数」と呼ぶ際には,2 階微分までの連続性を保証した滑らかな曲線を暗に意味する場合が多い.この理由は,現在最もよく使用されている「3 次の自然スプライン関数」が有する性質にある.3 次の自然スプライン関数は,与えられたデータ点を補間する際に,「2 階導関数の L2 ノルム」という意味での曲率を,他のどんなC2 級の関数よりも小さくすることができる.
この滑らかさに関する最適性と区分的多項式というモデルの単純性及び柔軟性から,スプライン関数は補間・平滑化・回帰分析といった基本問題から,Computer-Aided Design (CAD)・Computer Graphics (CG) といった応用に至るまで幅広い分野で使われている.
北原 大地,
“区分的多項式とスプライン関数の基礎—折れ線グラフを曲線にしてみよう—,”
日本音響学会誌, vol. 78, no. 10, pp. 570–577, Oct. 2022.
[Signal Processing Theory and Methods, Spline Smoothing] official access / pdf (preprint)
北原 大地,
“スプライン関数の基礎と分位点回帰への応用,”
電子情報通信学会信号処理研究会, Online, Aug. 2020, vol. 120, no. 142, pp. 37–42. (招待講演)
[Signal Processing Theory and Methods, Data Analysis, Spline Smoothing, Convex Optimization] official access / pdf (preprint)